硅谷面试经典算法之-线段树、树状数组
硅谷面试经典算法之-线段树、树状数组
线段树又叫Segmentation Tree,树状数组又叫Binary indexed tree (Fenwick tree)
他们都能在log(n)查询区间和,并且在log(n)时间内进行结点更新操作。
先认识下lowbit(x)函数
定义lowbit(x)为x的二进制表达式中最右边的1所对应的值。
比如,1234的二进制是0100 1101 0010 lowbit(1234)=2,在程序的实现中,
Lowbit(x)=x&-x;(为什么这样写呢?因为计算机内部采用补码表示,-x是x按位取反,尾数+1的结果)
树的结构图
让我们来看看图:横坐标是x, 纵坐标是lowbit(x)

对于节点x,
x如果为左子结点,则父结点的编号是x+lowbit(x),
x如果为右子结点,则父结点的编号是x-lowbit(x)
设C[i] 为以i结尾的水平长条内的元素之和,如c[6]=a5+a6。
顺着结点I往左走,边走边往上爬,沿途经过的c[i]所对应的长条不重复不遗漏的包含了所有需要累加的元素。
如sum(6) = c[6] + c[4]
如果修改了一个a[i] ,那么从c[i]往右走,边走边网上爬,沿途修改所有结点对应的c[i]即可。
如a[1] + 1 那么 c[1] + 1, c[2]+1,c[4]+1………一直到最大值。
面试常见题目:
[LintCode] Segment Tree Build 建立线段树
The structure of Segment Tree is a binary tree which each node has two attributes start and end denote an segment / interval.
start and end are both integers, they should be assigned in following rules:
The root’s start and end is given by build method.
The left child of node A has start= A.left, end=(A.left + A.right) / 2.
The right child of node A has start= (A.left + A.right) / 2 + 1, end=A.right.
if start equals to end, there will be no children for this node.
Implement
a build method with two parameters start and end, so that we can create
a corresponding segment tree with every node has the correct start and
end value, return the root of this segment tree.
Have you met this question in a real interview?
Yes
Clarification
Segment Tree (a.k.a Interval Tree) is an advanced data structure which can support queries like:
which of these intervals contain a given point
which of these points are in a given interval
Example
Given start=0, end=3. The segment tree will be:
[0, 3]
/ \
[0, 1] [2, 3]
/ \ / \
[0, 0] [1, 1] [2, 2] [3, 3]
Given start=1, end=6. The segment tree will be:
[1, 6]
/ \
[1, 3] [4, 6]
/ \ / \
[1, 2] [3,3] [4, 5] [6,6]
/ \ / \
[1,1] [2,2] [4,4] [5,5]
这道题让我们建立线段树,也叫区间树,是一种高级树结构,但是题目中讲的很清楚,所以这道题实现起来并不难,我们可以用递归来建立,写法很简单,参见代码如下(c++):
class Solution {
public:
/**
*@param start, end: Denote an segment / interval
*@return: The root of Segment Tree
*/
SegmentTreeNode * build(int start, int end) {
if (start > end) return NULL;
SegmentTreeNode *node = new SegmentTreeNode(start, end);
if (start < end) {
node->left = build(start, (start + end) / 2);
node->right = build((start + end) / 2 + 1, end);
}
return node;
}
};Range Sum Query - Mutable
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]
sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:
The array is only modifiable by the update function.
You may assume the number of calls to update and sumRange function is distributed evenly.
题解:
这
应该算是Range Query的经典题目之一了。也是通过这道题我第一次接触到了Segment Tree,也对Fenwick
Tree有了一点了解。下面是用Segment Tree来做的。 Segment
Tree线段树每一个节点都是一段线段,有start和end,然后还可以有其他的值,比如区间和sum,区间最大值max,区间最小值min。我们可以
用自底向上构建二叉树的方式构建Segment Tree,这个过程也有点类似于Bottom-up的merge sort,思想也是Divide
and Conquer。完毕之后就可以在O(logn)的时间update,或者得到range Sum。其实更好的方法是使用Fenwick
Tree, Fenwick Tree(Binary Indexed Tree)在处理Range
Query真的是一绝,构造简练,原理也精妙,还可以扩展到多维,一定要好好学一学。
Time Complexity - O(n) build, O(logn) update, O(logn) rangeSum, Space Complexity - O(n)
public class NumArray {
private class SegmentTreeNode {
public int start;
public int end;
public int sum;
public SegmentTreeNode left, right;
public SegmentTreeNode(int start, int end) {
this.start = start;
this.end = end;
this.sum = 0;
}
}
private SegmentTreeNode root;
public NumArray(int[] nums) {
this.root = buildTree(nums, 0, nums.length - 1);
}
public void update(int i, int val) {
update(root, i, val);
}
private void update(SegmentTreeNode node, int position, int val) {
if(node.start == position && node.end == position) {
node.sum = val;
return;
}
int mid = node.start + (node.end - node.start) / 2;
if(position <= mid) {
update(node.left, position, val);
} else {
update(node.right, position, val);
}
node.sum = node.left.sum + node.right.sum;
}
public int sumRange(int i, int j) {
return sumRange(root, i, j);
}
private int sumRange(SegmentTreeNode node, int lo, int hi) {
if(node.start == lo && node.end == hi) {
return node.sum;
}
int mid = node.start + (node.end - node.start) / 2;
if(hi <= mid) {
return sumRange(node.left, lo, hi);
} else if (lo > mid) {
return sumRange(node.right, lo, hi);
} else {
return sumRange(node.left, lo, mid) + sumRange(node.right, mid + 1, hi);
}
}
private SegmentTreeNode buildTree(int[] nums, int lo, int hi) {
if(lo > hi) {
return null;
} else {
SegmentTreeNode node = new SegmentTreeNode(lo, hi);
if(lo == hi) {
node.sum = nums[lo];
} else {
int mid = lo + (hi - lo) / 2;
node.left = buildTree(nums, lo, mid);
node.right = buildTree(nums, mid + 1, hi);
node.sum = node.left.sum + node.right.sum;
}
return node;
}
}
}
// Your NumArray object will be instantiated and called as such:
// NumArray numArray = new NumArray(nums);
// numArray.sumRange(0, 1);
// numArray.update(1, 10);
// numArray.sumRange(1, 2);Fenwick Tree: (Binary Indexed Tree) (树状数组)
很
有意思的构建,以数组nums = {1, 2, 3, 4, 5, 6, 7, 8}为例,这个数组长度为8。 跟dynamic
programming的预处理很像,我们先建立一个长度为nums.length + 1 =
9的数组BIT。接下来遍历数组nums,对BIT数组进行update(i + 1,
nums[i])。这里BIT数组每个值BIT[i]代表nums数组里在i之前的部分元素和。原理是像自然数可以被表示为2n的和一样,把nums数组
里到0到i的sum表示成2n的和,从而导致update和rangeSum都可以用O(logn)的时间求出来。这里构建的时候可以有几种写法,主要就
是利用当前i的least significante
1来确定到底BIT[i]要保存多少原数组的值。这里借用algorithmist的原话”Every index in the cumulative
sum array, say i, is responsible for the cumulative sum from the index i
to (i - (1<<r) + 1)。” 构建过程中可以用 (i & -i)来找到least significate
1,之后来进行i = i + (i & -i)来尝试从小到大计算下一个BIT数组中被影响的元素。 而rangeSum的时候则使用i = i
- (i & -i)来从大到小查找从0到i - 1的sum。
构建过程 - update, 给定数组nums = {1,2, 3, 4, 5, 6, 7, 8}
BIT[0] = 0
BIT[1] = nums[0] = 1 = 1
BIT[2] = nums[0] + nums[1] = 1 + 2 = 3
BIT[3] = nums[2] = 3 = 3
BIT[4] = nums[0] + nums[1] + nums[2] + nums[3] = 1+ 2 + 3 + 4 = 10
BIT[5] = nums[4] = 5 = 5
BIT[6] = nums[4] + nums[5] = 5 + 6 = 11
BIT[7] = nums[6] = 7 = 7
BIT[8] = nums[0] + nums[1] + nums[2] + nums[3] + nums[4] + nums[5] + nums[6] + nums[7] = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36
求Sum过程, 通过 sum = BIT[i + 1]; i = i - (i & -i); 从大到小迭代来计算。
sum(0) = BIT[1]
sum(1) = BIT[2]
sum(2) = BIT[3] + BIT[2]
sum(3) = BIT[4]
sum(4) = BIT[5] + BIT[4]
sum(5) = BIT[6] + BIT[4]
sum(6) = BIT[7] + BIT[6] + BIT[4]
sum(7) = BIT[8]
得到sum(i)以后就可以相减来计算range sum了。
Time Complexity - O(nlogn) build, O(logn) update, O(logn) rangeSum, Space Complexity - O(n)
public class NumArray {
private int BIT[]; // Binary Indexed Tree = Fenwick Tree
private int[] nums;
public NumArray(int[] nums) {
BIT = new int[nums.length + 1];
for(int i = 0; i < nums.length; i++) {
init(i + 1, nums[i]);
}
this.nums = nums;
}
private void init(int i, int val) {
while(i < BIT.length) {
BIT[i] += val;
i = i + (i & -i);
}
}
public void update(int i, int val) {
int delta = val - nums[i];
nums[i] = val;
init(i + 1, delta);
}
public int sumRange(int i, int j) {
return getSum(j + 1) - getSum(i);
}
private int getSum(int i) {
int sum = 0;
while(i > 0) {
sum += BIT[i];
i = i - (i & -i);
}
return sum;
}
}Range Sum Query 2D - Mutable
题目:
Given
a 2D matrix matrix, find the sum of the elements inside the rectangle
defined by its upper left corner (row1, col1) and lower right corner
(row2, col2).
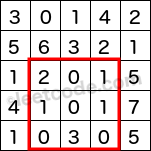
The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Example:
Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
update(3, 2, 2)
sumRegion(2, 1, 4, 3) -> 10
Note:
The matrix is only modifiable by the update function.
You may assume the number of calls to update and sumRegion function is distributed evenly.
You may assume that row1 ≤ row2 and col1 ≤ col2.
链接: http://leetcode.com/problems/range-sum-query-2d-mutable/
题解:
二
维Range Sum Query mutable,原理是要构建一个2D Segment Tree或者 2D Fenwick
Tree。由于上一题是先做的Segment Tree,这回也先写2D Segment Tree。构建2D Segment
Tree依然是使用Divide and Conquer,我们要把整个平面分成4个部分,所以2D Segment Tree也是一个Quad
Tree,每个节点有四个子节点,NW, NE, SW, SE, 节点的sum是四个子节点的sum。这样我们就可以用与1D Segment
Tree类似的方法来写rangeSum以及update。要注意rangeSum时的判断,有好几种情况,比较复杂。
public class NumMatrix {
private class SegmentTreeNode2D {
public int tlRow;
public int tlCol;
public int brRow;
public int brCol;
public int sum;
public SegmentTreeNode2D nw, ne, sw, se;
public SegmentTreeNode2D(int tlRow, int tlCol, int brRow, int brCol) {
this.tlRow = tlRow;
this.tlCol = tlCol;
this.brRow = brRow;
this.brCol = brCol;
this.sum = 0;
}
}
public SegmentTreeNode2D root;
public NumMatrix(int[][] matrix) {
if(matrix == null || matrix.length == 0) {
return;
}
root = buildTree(matrix, 0, 0, matrix.length - 1, matrix[0].length - 1);
}
public void update(int row, int col, int val) {
update(root, row, col, val);
}
private void update(SegmentTreeNode2D node, int row, int col, int val) {
if(node.tlRow == row && node.brRow == row && node.tlCol == col && node.brCol == col) {
node.sum = val;
return;
}
int rowMid = node.tlRow + (node.brRow - node.tlRow) / 2;
int colMid = node.tlCol + (node.brCol - node.tlCol) / 2;
if(row <= rowMid) {
if(col <= colMid) {
update(node.nw, row, col, val);
} else {
update(node.ne, row, col, val);
}
} else {
if(col <= colMid) {
update(node.sw, row, col, val);
} else {
update(node.se, row, col, val);
}
}
node.sum = 0;
if(node.nw != null) {
node.sum += node.nw.sum;
}
if(node.ne != null) {
node.sum += node.ne.sum;
}
if(node.sw != null) {
node.sum += node.sw.sum;
}
if(node.se != null) {
node.sum += node.se.sum;
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return sumRegion(root, row1, col1, row2, col2);
}
private int sumRegion(SegmentTreeNode2D node, int tlRow, int tlCol, int brRow, int brCol) {
if(node.tlRow == tlRow && node.tlCol == tlCol && node.brRow == brRow && node.brCol == brCol) {
return node.sum;
}
int rowMid = node.tlRow + (node.brRow - node.tlRow) / 2;
int colMid = node.tlCol + (node.brCol - node.tlCol) / 2;
if(brRow <= rowMid) { // top-half plane
if(brCol <= colMid) { // north-west quadrant
return sumRegion(node.nw, tlRow, tlCol, brRow, brCol);
} else if(tlCol > colMid) { // north-east quadrant
return sumRegion(node.ne, tlRow, tlCol, brRow, brCol);
} else { // intersection between nw and ne
return sumRegion(node.nw, tlRow, tlCol, brRow, colMid) + sumRegion(node.ne, tlRow, colMid + 1, brRow, brCol);
}
} else if(tlRow > rowMid) { // bot-half plane
if(brCol <= colMid) { // south-west quadrant
return sumRegion(node.sw, tlRow, tlCol, brRow, brCol);
} else if(tlCol > colMid) { // south-east quadrant
return sumRegion(node.se, tlRow, tlCol, brRow, brCol);
} else { //intersection between sw and sw
return sumRegion(node.sw, tlRow, tlCol, brRow, colMid) + sumRegion(node.se, tlRow, colMid + 1, brRow, brCol);
}
} else { // full-plane intersection
if(brCol <= colMid) { // left half plane
return sumRegion(node.nw, tlRow, tlCol, rowMid, brCol) + sumRegion(node.sw, rowMid + 1, tlCol, brRow, brCol) ;
} else if(tlCol > colMid) { // right half plane
return sumRegion(node.ne, tlRow, tlCol, rowMid, brCol) + sumRegion(node.se, rowMid + 1, tlCol, brRow, brCol) ;
} else { // full-plane intersection
return sumRegion(node.nw, tlRow, tlCol, rowMid, colMid)
+ sumRegion(node.ne, tlRow, colMid + 1, rowMid, brCol)
+ sumRegion(node.sw, rowMid + 1, tlCol, brRow, colMid)
+ sumRegion(node.se, rowMid + 1, colMid + 1, brRow, brCol);
}
}
}
private SegmentTreeNode2D buildTree(int[][] matrix, int tlRow, int tlCol, int brRow, int brCol) {
if(tlRow > brRow || tlCol > brCol) {
return null;
} else {
SegmentTreeNode2D node = new SegmentTreeNode2D(tlRow, tlCol, brRow, brCol);
if(tlRow == brRow && tlCol == brCol) {
node.sum = matrix[tlRow][tlCol];
} else {
int rowMid = tlRow + (brRow - tlRow) / 2;
int colMid = tlCol + (brCol - tlCol) / 2;
node.nw = buildTree(matrix, tlRow, tlCol, rowMid, colMid);
node.ne = buildTree(matrix, tlRow, colMid + 1, rowMid, brCol);
node.sw = buildTree(matrix, rowMid + 1, tlCol, brRow, colMid);
node.se = buildTree(matrix, rowMid + 1, colMid + 1, brRow, brCol);
node.sum = 0;
if(node.nw != null) {
node.sum += node.nw.sum;
}
if(node.ne != null) {
node.sum += node.ne.sum;
}
if(node.sw != null) {
node.sum += node.sw.sum;
}
if(node.se != null) {
node.sum += node.se.sum;
}
}
return node;
}
}
}
// Your NumMatrix object will be instantiated and called as such:
// NumMatrix numMatrix = new NumMatrix(matrix);
// numMatrix.sumRegion(0, 1, 2, 3);
// numMatrix.update(1, 1, 10);
// numMatrix.sumRegion(1, 2, 3, 4);2D Segment Tree: Time Complexity - O(mn) build,O(logmn) update, O(logmn) rangeSum , Space Complexity - O(mn) 复杂度算得不是很清楚,很可能不正确,二刷再继续改正。
public class NumArray {
private SegmentTreeNode root;
private int[] nums;
public NumArray(int[] nums) {
this.nums = nums;
this.root = buildTree(0, nums.length - 1);
}
void update(int i, int val) {
update(root, i, val);
}
private void update(SegmentTreeNode node, int pos, int val) {
if (node == null) return;
if (node.start == pos && node.end == pos) {
node.val = val;
nums[pos] = val;
return;
}
int mid = node.start + (node.end - node.start) / 2;
if (pos <= mid) {
update(node.left, pos, val);
} else {
update(node.right, pos, val);
}
node.val = node.left.val + node.right.val;
}
public int sumRange(int i, int j) {
return sumRange(root, i, j);
}
private int sumRange(SegmentTreeNode node, int lo, int hi) {
if (lo > hi) return 0;
if (node.start == lo && node.end == hi) return node.val;
int mid = node.start + (node.end - node.start) / 2;
if (hi <= mid) {
return sumRange(node.left, lo, hi);
} else if (lo > mid) {
return sumRange(node.right, lo, hi);
} else {
return sumRange(node.left, lo, mid) + sumRange(node.right, mid + 1, hi);
}
}
private SegmentTreeNode buildTree(int lo, int hi) {
if (lo > hi) return null;
SegmentTreeNode node = new SegmentTreeNode(lo, hi);
if (lo == hi) {
node.val = nums[lo];
} else {
int mid = lo + (hi - lo) / 2;
node.left = buildTree(lo, mid);
node.right = buildTree(mid + 1, hi);
node.val = node.left.val + node.right.val;
}
return node;
}
private class SegmentTreeNode {
int start;
int end;
int val;
SegmentTreeNode left, right;
public SegmentTreeNode(int start, int end) {
this.start = start;
this.end = end;
this.val = 0;
}
}
}
// Your NumArray object will be instantiated and called as such:
// NumArray numArray = new NumArray(nums);
// numArray.sumRange(0, 1);
// numArray.update(1, 10);
// numArray.sumRange(1, 2);In-place Fenwick tree, beats 100% java submissions
public class NumMatrix {
private final int[][] matrix;
private final int numRows;
private final int numCols;
public NumMatrix(int[][] matrix) {
this.matrix = matrix;
numRows = matrix.length;
numCols = (numRows > 0) ? matrix[0].length : 0;
initTree();
}
public void update(int row, int col, int val) {
int prev = getTreeSum(row, col);
if (col > 0)
prev -= getTreeSum(row, col - 1);
if (row > 0)
prev -= getTreeSum(row - 1, col);
if (row > 0 && col > 0)
prev += getTreeSum(row - 1, col - 1);
int delta = val - prev;
updateTree(row, col, delta);
}
private void initTree() {
for (int i = 1; i <= numRows; i++) {
for (int j = 1; j <= numCols; j++) {
int jParent = j + (j & (-j));
if (jParent <= numCols) {
matrix[i - 1][jParent - 1] += matrix[i - 1][j - 1];
}
}
}
for (int j = 1; j <= numCols; j++) {
for (int i = 1; i <= numRows; i++) {
int iParent = i + (i & (-i));
if (iParent <= numRows) {
matrix[iParent - 1][j - 1] += matrix[i - 1][j - 1];
}
}
}
}
private void updateTree(int row, int col, int val) {
for (int i = row + 1; i <= numRows; i += i & (-i)) {
for (int j = col + 1; j <= numCols; j += j & (-j)) {
matrix[i - 1][j - 1] += val;
}
}
}
private int getTreeSum(int row, int col) {
int sum = 0;
for (int i = row + 1; i > 0; i -= i & (-i)) {
for (int j = col + 1; j > 0; j -= j & (-j)) {
sum += matrix[i - 1][j - 1];
}
}
return sum;
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int sum = getTreeSum(row2, col2);
if (row1 > 0)
sum -= getTreeSum(row1 - 1, col2);
if (col1 > 0)
sum -= getTreeSum(row2, col1 - 1);
if (col1 > 0 && row1 > 0)
sum += getTreeSum(row1 - 1, col1 - 1);
return sum;
}
}鸣谢大神们
细雨呢喃:https://www.hrwhisper.me/binary-indexed-tree-fenwick-tree/
Topcode: https://www.topcoder.com/community/data-science/data-science-tutorials/binary-indexed-trees/
Grandyang 仰天长啸仗剑红尘,冬去春来寒暑几更…
http://www.cnblogs.com/grandyang/p/5659314.html
YRB
http://www.cnblogs.com/yrbbest/p/5056739.html
Wikipedia: Segment Tree
Lintcode Leetcode 大神Raaar
微信长按扫码加美国加群小助手订阅号

微信长按扫码加北美加群小助手服务号

微信扫一扫
关注该公众号
